Mathematical Proof that 3=5 Any Math Wizzes Here?

[crait]

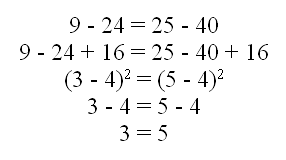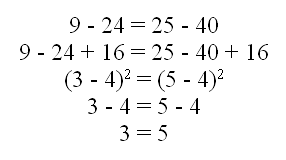
Define the equality.
Add a constant (16) to each side.
Express the equality as a binomial.
Take the square root of each side.
Add a constant (4) to each side.

What do you guys think of this?

 

[LaSombra]

well, (3-4)^2 is gonna be one because a negative x negative = pos

so they're going by a -1 = +2 in order to prove that 3=5

 

[crait]

Quote:
But they're doing the math correctly.
They start out with two things that are equal but keep going until they get 3 = 5. I guess they could have stopped after making the two sides of the river binomials and said 1 = -1. (That has a difference of 2. Same as 3=5)
I can't think of any postulates or theorems that negate this event.

 

[LaSombra]

Quote:
But they're doing the math correctly.
They start out with two things that are equal but keep going until they get 3 = 5. I guess they could have stopped after making the two sides of the river binomials and said 1 = -1. (That has a difference of 2. Same as 3=5)
I can't think of any postulates or theorems that negate this event.

yeah but the square root of any number will always be a positive and a negative, two possibilities. Square root of 16 is 4, but it is also -4, etc

 

[key west chick]

 

[crait]

Quote:
But they're doing the math correctly.
They start out with two things that are equal but keep going until they get 3 = 5. I guess they could have stopped after making the two sides of the river binomials and said 1 = -1. (That has a difference of 2. Same as 3=5)
I can't think of any postulates or theorems that negate this event.

yeah but the square root of any number will always be a positive and a negative, two possibilities. Square root of 16 is 4, but it is also -4, etc

Yes, that is true but you're forgetting that whenever you have an equation like this, with squares on both sides, don't you just remove the squares?
Like if you had the square root of x squared. You would just remove both the square and the square root. Right?

 

[Beekissed]

I know for a fact that , at times, 3=5.

Case in point:

My teen says he needs $3 for something at school and I only have a $5 bill in my wallet. Regardless of the need for only $3 for this item, I never get $2 in change.......so..in effect, $3=$5 in my life quite frequently.

I guess I'm not much of a math whiz but my son is going to go places in the financial world, I guarantee it!

Possibly to jail....

 

[okiegirl]

wow! I have never felt more dumb in my life.

 

[19hhbelgian]

Quote:

LOVE IT!!!!!

 

[PineBurrowPeeps]

You people are speaking greek.